K-matrix¶
Note
Implementation of the \(K\)-matrix is currently further worked out in [TR-005] K-matrix.
While ampform does not yet provide a generic way to produce an amplitude model with \(K\)-matrix dynamics, it is fairly simple to produce an expression for the \(K\)-matrix and play around with it interactively.
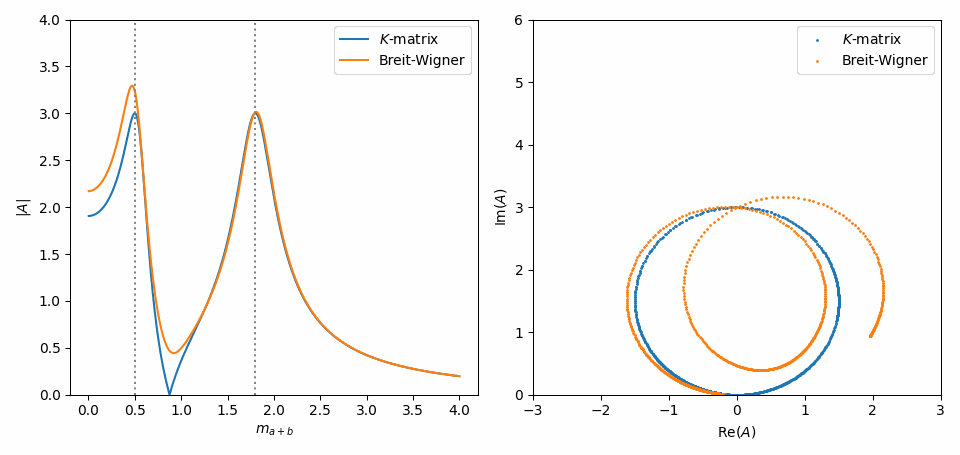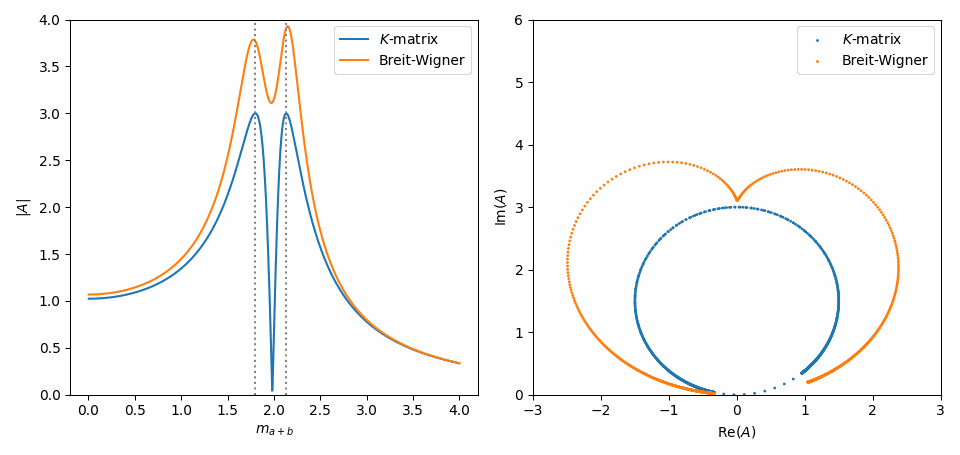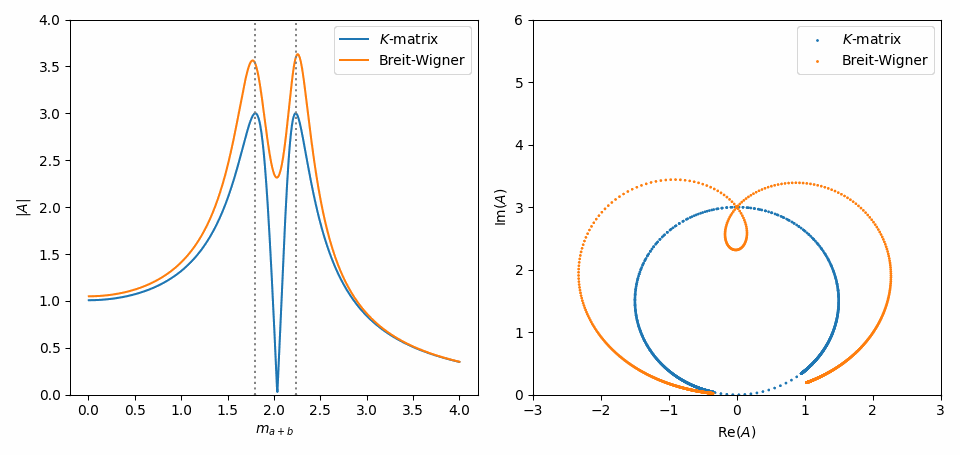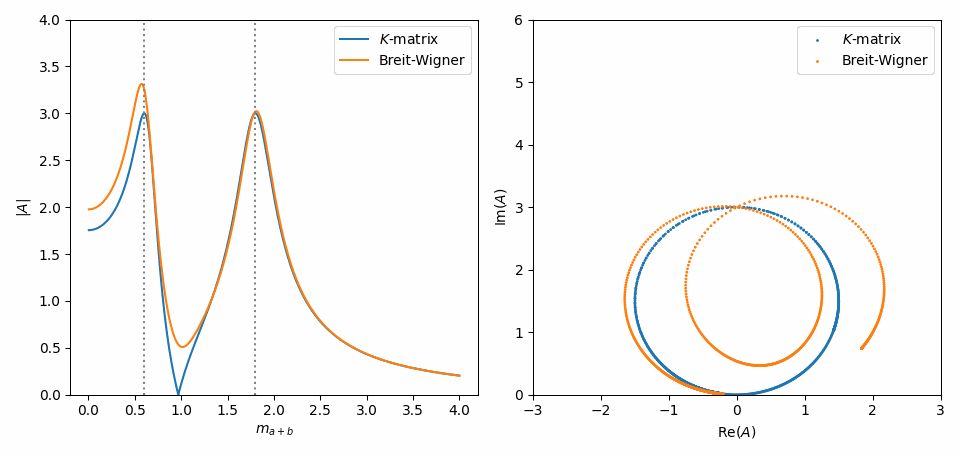
This notebook shows how a \(K\)-matrix for one channel with two poles compares to using a sum of two Breit-Wigner functions. For more info on the \(K\)-matrix, see this instructive presentation Meyer 2008, or the classic paper Chung et al. 1995.
Amplitude definition¶
A \(K\)-matrix for two poles and one channel can be parametrized as follows:
import sympy as sp
L = sp.Symbol("L", integer=True)
m_a, m_b, d = sp.symbols("m_a m_b d")
from ampform.dynamics import coupled_width
def kmatrix_term(m, m1, gamma1, m2, gamma2):
running_gamma1 = coupled_width(m ** 2, m1, gamma1, m_a, m_b, L, d)
running_gamma2 = coupled_width(m ** 2, m2, gamma2, m_a, m_b, L, d)
return (m1 * running_gamma1) / (
(m1 ** 2 - m ** 2)
- sp.I * m1 * running_gamma1
- sp.I * (m1 ** 2 - m ** 2) / (m2 ** 2 - m ** 2) * m2 * running_gamma2
)
c1, c2, phi1, phi2 = sp.symbols("c1, c2, phi1, phi2")
a1 = c1 * sp.exp(sp.I * phi1)
a2 = c2 * sp.exp(sp.I * phi2)
m, m1, m2, gamma1, gamma2 = sp.symbols("m, m1, m2, Gamma1, Gamma2")
term1 = kmatrix_term(m, m1, gamma1, m2, gamma2)
term2 = kmatrix_term(m, m2, gamma2, m1, gamma1)
kmatrix = a1 * term1 + a2 * term2
running_gamma1 = coupled_width(m ** 2, m1, gamma1, m_a, m_b, L, d)
running_gamma2 = coupled_width(m ** 2, m2, gamma2, m_a, m_b, L, d)
kmatrix.subs(
{
running_gamma1: sp.Symbol(R"\Gamma_{1}(m)"),
running_gamma2: sp.Symbol(R"\Gamma_{2}(m)"),
},
)
where \(\Gamma(m)\) is the coupled_width().
Two Breit-Wigner ‘poles’ with the same parameters would look like this (making use of relativistic_breit_wigner_with_ff()):
from ampform.dynamics import relativistic_breit_wigner_with_ff
term1 = relativistic_breit_wigner_with_ff(m ** 2, m1, gamma1, m_a, m_b, L, d)
term2 = relativistic_breit_wigner_with_ff(m ** 2, m2, gamma2, m_a, m_b, L, d)
bw = a1 * term1 + a2 * term2
from ampform.dynamics import BlattWeisskopfSquared, breakup_momentum_squared
q_squared = breakup_momentum_squared(m ** 2, m_a, m_b)
ff2 = BlattWeisskopfSquared(L, z=q_squared * d ** 2)
bw.subs(
{
running_gamma1: sp.Symbol(R"\Gamma_{1}(m)"),
running_gamma2: sp.Symbol(R"\Gamma_{2}(m)"),
sp.sqrt(ff2): sp.Symbol("B_{L}(q)"),
},
)
with \(B_L(q)\) a Blatt-Weisskopf barrier factor (see BlattWeisskopfSquared) and \(q(m)\) the breakup_momentum_squared().
Prepare sliders¶
Just like in Inspect model interactively, we use symplot to generate sliders for the Symbols in both expressions:
from symplot import prepare_sliders
np_kmatrix, sliders = prepare_sliders(kmatrix.doit(), m)
set(sliders)
{'Gamma1',
'Gamma2',
'L',
'c1',
'c2',
'd',
'm1',
'm2',
'm_a',
'm_b',
'phi1',
'phi2'}
Luckily, the dummy variables for the lambdified argument should be the same (the symbol names are valid identifiers), so as long as we use the same order of the positional arguments, we can lambdify() the sum of Breit-Wigners in the same way:
np_bw = sp.lambdify(
(m, gamma1, gamma2, L, c1, c2, d, m1, m2, m_a, m_b, phi1, phi2),
bw.doit(),
"numpy",
)
Again, we need to identify how we want to plot these (complex) amplitudes:
def abs_amplitude_bw(plot_variable, **kwargs):
values = np_bw(plot_variable, **kwargs)
return np.abs(values)
def argand_bw(**kwargs):
values = np_bw(plot_domain, **kwargs)
argand = np.array([values.real, values.imag])
return argand.T
def abs_amplitude_kmatrix(plot_variable, **kwargs):
values = np_kmatrix(plot_variable, **kwargs)
return np.abs(values)
def argand_kmatrix(**kwargs):
values = np_kmatrix(plot_domain, **kwargs)
argand = np.array([values.real, values.imag])
return argand.T
We also need to define a domain over which to plot the invariant mass:
import numpy as np
plot_domain = np.linspace(0, 4, 1_000)
…as well as ranges and (optionally) initial values for the sliders:
sliders.set_ranges(
c1=(0, 5),
c2=(0, 5),
phi1=(0, 2 * sp.pi, 40),
phi2=(0, 2 * sp.pi, 40),
m1=(0, 3, 100),
m2=(0, 3, 100),
Gamma1=(0, 2, 100),
Gamma2=(0, 2, 100),
m_a=(0, 1),
m_b=(0, 1),
L=(0, 8),
d=(0, 5),
)
sliders.set_values(
c1=3,
c2=3,
phi1=0,
phi2=0,
m1=1.2,
m2=1.8,
Gamma1=0.3,
Gamma2=0.4,
L=0,
d=1,
)
Compare Breit-Wigner and K-matrix¶
That’s it. Now, we do the same as in Inspect model interactively, but with some slight adaptations to combine the \(K\)-matrix and Breit-Wigner formulations of both amplitudes in one plot. Notice in the Argand plot how the \(K\)-matrix preserves unitarity, while the Breit-Wigners do not!
%matplotlib widget
import matplotlib.pyplot as plt
import mpl_interactions.ipyplot as iplt
# Create figure
fig, axes = plt.subplots(
1, 2, figsize=1.2 * np.array((8, 3.8)), tight_layout=True
)
# fig.suptitle(R"$J/\psi \to \gamma f_0, f_0 \to \pi^0\pi^0$")
ax_intensity, ax_argand = axes
m_label = "$m_{a+b}$"
ax_intensity.set_xlabel(m_label)
ax_intensity.set_ylabel("$|A|$")
ax_argand.set_xlabel("Re($A$)")
ax_argand.set_ylabel("Im($A$)")
# Intensity
controls = iplt.plot(
plot_domain,
abs_amplitude_kmatrix,
label="$K$-matrix",
**sliders,
ylim="auto",
ax=ax_intensity,
)
iplt.plot(
plot_domain,
abs_amplitude_bw,
label="Breit-Wigner",
controls=controls,
ylim="auto",
ax=ax_intensity,
)
plt.legend(loc="upper right")
iplt.axvline(controls["m1"], c="gray", linestyle="dotted")
iplt.axvline(controls["m2"], c="gray", linestyle="dotted")
# Argand plots
iplt.scatter(
argand_kmatrix,
label="$K$-matrix",
controls=controls,
parametric=True,
s=1,
ax=ax_argand,
)
iplt.scatter(
argand_bw,
label="Breit-Wigner",
controls=controls,
parametric=True,
s=1,
ax=ax_argand,
)
plt.legend(loc="upper right");